THIRD GENERATION MUOGRPHY OBSERVATION SYSTEM (2016) The University of Tokyo, Wigner Research Centre for Physics of the Hungarian Academy of Sciences, and Toshiyuki Kita (Design) This system enables us to image large-sized objects with an angular resolution of better than 3 mrad.

PLASTIC SCINTILLATOR IN THE LEGENDARY EINSTEIN ELEVATOR (2018) Hideaki Miyamoto

CELESTIAL GLOBE (2018) Yuji Ichikawa A precipitations of muons from the upper hemisphere can be experienced by inserting your head into the globe.

PHOENIX (2018) Keizaburo Okamoto A number of holes of the phoenix looks through objects with muography.

PION DECAY (2016) Hiroyuki Sekioka Pions decay into muons.

MUOGRAPHY (2016) Agnes Husz Performance art piece in one of the ground floor rooms incorporating projected video and sound art accompanying sessions of ceramic art construction conducted live in front of audiences.

2ND GENERATION MUOGRAPHY OBSERVATION SYSTEM (2015) Hiroyuki Sekioka (Photogaph) Plastic-scintillator-based muography observation system

EYE OF MUOGRAPHY (2018) Hiroshi Nakajima

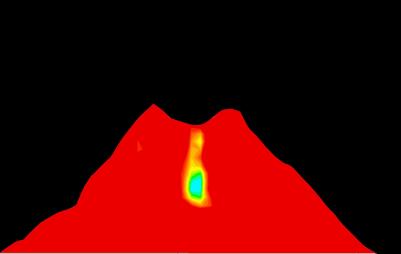MAGMA CONVECTION (2017) Hiroyuki Tanaka Muographic image of magma convection in Satsuma-Iwojima volcano. リンク

STATISTIC VOLCANO (2017) Sara Steigerwald Statistics are essential in order to interpret the number of muon counts in muography data. If the number of muon counts is not sufficient, it is difficult for us to be confident that the number represents the true structure within and is not simply a coincidental fluctuation. The number of counts itself is a fact, but the factor that governs this number becomes probabilistic. If the muon counts are smaller, coincidental fluctuations are often errors and tend to be relatively large. As a metaphor, let`s imagine that the muon counts are instead a count of the number of customers visiting a newly remodeled cafe. If the owner noticed an increase of 2 customers per day before the reopening and then 3 customers per day after reopening, it would be difficult to confidently conclude that the increase was due to the remodeling. However, if it increased from 2000 customers to 3000 customers, the confidence level would increase even though in both cases before and after the remodeling there was the same level of increase: the second day being 1.5 times more than the first day. The confidence level is different between them since the amount of customers counted is different. Similarly, in order to visualize the internal structure of a volcano with higher precision, it is necessary for us not only to increase the image resolution but also to increase the number of muon counts recorded in each pixel of the image. To achieve this increased number it is usually necessary to increase the size of the active area, usually by increasing the size of the muography observation system (the muon detector) so more muon events can be collected. This painting shows a volcano composed of dice, depicting muon counts and their dependence on statistics. The number of counts necessary to reveal the mystery of what lies within the volcano interior is equivalent to the number of times one throws a slightly asymmetric (or loaded) dice. If we have only a small amount of muon counts, we might have to overlook data that include regional information with an unexpected low-density inside the volcano. However, as we accumulate a larger number of muon counts, our confidence level in these data will increase.

VOLCANO (2018) Sara Steigerwald Of all the geodynamic elements of the Earth, one of the most dramatic is the volcano since during eruptions we can see undergroundoriginated phenomenon visibly rise out onto the surface of the earth and into the atmosphere. Until recently only lava and processes during and after volcanic eruptions were observed with magma and the cycles of movement within the volcano being invisible and unknown. With muography, now the movements of the magma can be visualized which helps researchers understand the processes leading to eruptions. This painting depicts bubbly magma that was imaged by muography in the Japanese volcano, Satsuma Iwojima. The step-like structure that can be seen in the ridge region of this painting visually indicates the image resolution of current muography. If muography images could become higher resolution, more information about the magma could be extracted from images. The shape of the magma pathway inside the volcano can indicate the way in which the eruption will occur. Therefore, if we could get faster and more accurate images, we would be able to better predict and study the unseen processes going on within volcanoes. There is a lot of motivation to improve this technology. Ongoing developments in 3rd generation muography are expected to create images with much higher resolution.

MUOGRAPHY SYMPHONY (2018) Federico Iacobucci

MUOGRAPHERS (2017) Satoshi Hashimoto (Photograph)

DRAGON (2018) Yoshiyuki Nakano

MUOGRAPHIC OBSERVATION (2008) Etsuro Koyama (Photograph)

COMPACT MUON SOLENOID (2016) Michael Hoch

MUOGRAPHY T-SHIRTS (2016) Hiroyuki Sekioka (Design)

VOID UNDERNEATH LAVA (2007) Hiroyuki Tanaka

MUON DREAM FLIGHT (2018) Fumio Sato Muons’ travel starts somewhere in the universe. It can be an eternal tour without a goal, but f they can reach the Earth, some of them may can find their goal. This piece depicts from the universe to the Earth’s core. Can magma be their goal?

LIGHT PARTICLES (2018) Hiroko Hashimoto

TIMESPACE (2018) Mako Nishino Over the horizon, Over the galaxy, Arriving from the universe, Penetrating me, Becoming the time space window, and Going back to the universe.

MUOGRAPHY (2018) Akihiro Kubota (Space design)

CERENKOV CONES (2018) Mitsuo Matsuda

VOLCANO SLICES (2018) Hiroyuki Tanaka

RELATIVISTIC HOURGLASS (2017) Sara Steigerwald Albert Einstein constructed the theory of special relativity based on the idea of the invariance of the speed of light. This principle means that if we follow the light, the relative speed between the follower and light will not change. In short, the follower will never be able to pass the light. In order for this puzzling principle to apply in all circumstances, we have to adjust space and time. This is because speed is defined as the distance traveled in a certain time; for example the speed of light is 300,000,000 meters (7.5 times longer than the circumference of the Earth’s equator) per second. More in detail, when an observer I at rest observes another observer II moving from the static position A to the static position B, since the distance between A and B will not change for Observer I, the time of Observer II must be changed. Alternatively, the time will not be changed for Observer II, the distance between A and B must be changed. This changing rate can be quantitatively expressed, and it will be (1- v2/c2)1/2, where v is the observer’s velocity and c is the seed of light. This formula indicates that the speed of clock ticks or length contraction will asymptotically approaches to zero. The hourglass in this figure represents time. The conventional shaped smaller hourglass (on the left with yellow sand) shows how we experience time in our daily life while the larger distorted hourglass represents “stretched time” and “Lorentz contracted hourglass”. Accordingly, there is more sand remaining in the hourglass of “relativistic time.”

THREADS OF A VOLCANO (2018) Hiroshi Nakajima

UNDERGROUND ANCIENT CITY DETECTION (2016) Giulio Saracino

BUDAPEST UNDERGROUND (2015) Laszlo Olah and Dezso Varga

MUON PRODUCTION AND DECAY (2016) Hiroyuki Sekioka

SECONDARY COSMIC RAYS (2016) Hiroyuki Sekioka

MUON TRAVELS THROUGH MATTER (2018) Sara Steigerwald If we could watch a muon as it slams into the volcano and interacts with the atoms within, what would we see? Since our eyes cannot see muons, we have to use our imagination to visualize the idea. Through interaction with atoms in a volcano, muons will emit and absorb light that is composed of photons. Therefore, the region around the muon is filled with light. However, this light has much higher energies than visible light so it would be impossible for people to see, A representation of this idea, is imagined in this painting. The local region near the muon is being lit by invisible photons as a muon interacts.

BUBLY MAGMA (2017) Sara Steigerwald Bubbly magma in the shallow conduit of Satsuma-Iwojima volcano. The magma convection hypothesis was proposed to explain the volcanic gas observation results. Muography revealed the low density conduit near the ground surface. This result indicated that the deep underground magma chamber is connected to the region near the ground surface and convection occurs between them. This figure is linked to FIG2, and shows bubbly magma revealed with muography in conjunction with the muon passing through Satsum-Iwojima volcano.

PENETRATION TO OBJECTS (2017) Sara Steigerwald It has been established that the penetration power of muons is much stronger than the x ray after various underground particle measurement experiments. This figure shows muons penetrating the object from the right to the left. The number of penetrated and terminated muons varies depending on the thickness and density of the object.

ASAMA MUOGRAPHY II (2017) Sara Steigerwald The formula indicated on the bottom right side of the first figure shows the Lorentz invariant of muons that pass through the volcano. The muon’s invariant mass (mm) is expressed by the muon’s energy (Em) and momentum (pm). This formula infers relativistic muons are passing through the shallow part of the volcano.

INTERACTIONS (2017) Hiroyuki Sekioka Electron’s radiation length and the Feynman diagram for muon’s bremsstrahlung in matter. Muons emit electromagnetic waves and subsequently absorb photons from nuclei.

VOLCANO MUOGRAPHY (2017) Hiroshi Nakajima

MUOGRPHIC SIGNALS (2017) Hiroyuki Sekioka

EQUATIONS (2017) Hiroyuki Sekioka (Photograph)

DIVISIBILITY OF OBJECTS (2017) Sara Steigerwald Our everyday experience shows us any objects can be divided into various shapes and sizes. If we magnify the divided pieces, various shapes and sizes appear; further divisions and stronger magnification yield the same results, which seem to suggest that this process could repeated endlessly. However once this assumption was questioned and the controversial concept of atomism was adopted by the academic community, new discoveries and theories in the field of natural science became possible.

MUOGRAPHERS (2017) Satoshi Hashimoto